Cooperation tends to pay, in the long run

Game theory is a field of mathematics concerned with modelling strategic decision making. It’s of interest to computer scientists, economists, political scientists, and business strategists and negotiators. Game theory enjoyed some brief pop culture recognition when Russel Crowe played mathematician John Nash in 2001’s Best Picture winning A Beautiful Mind.

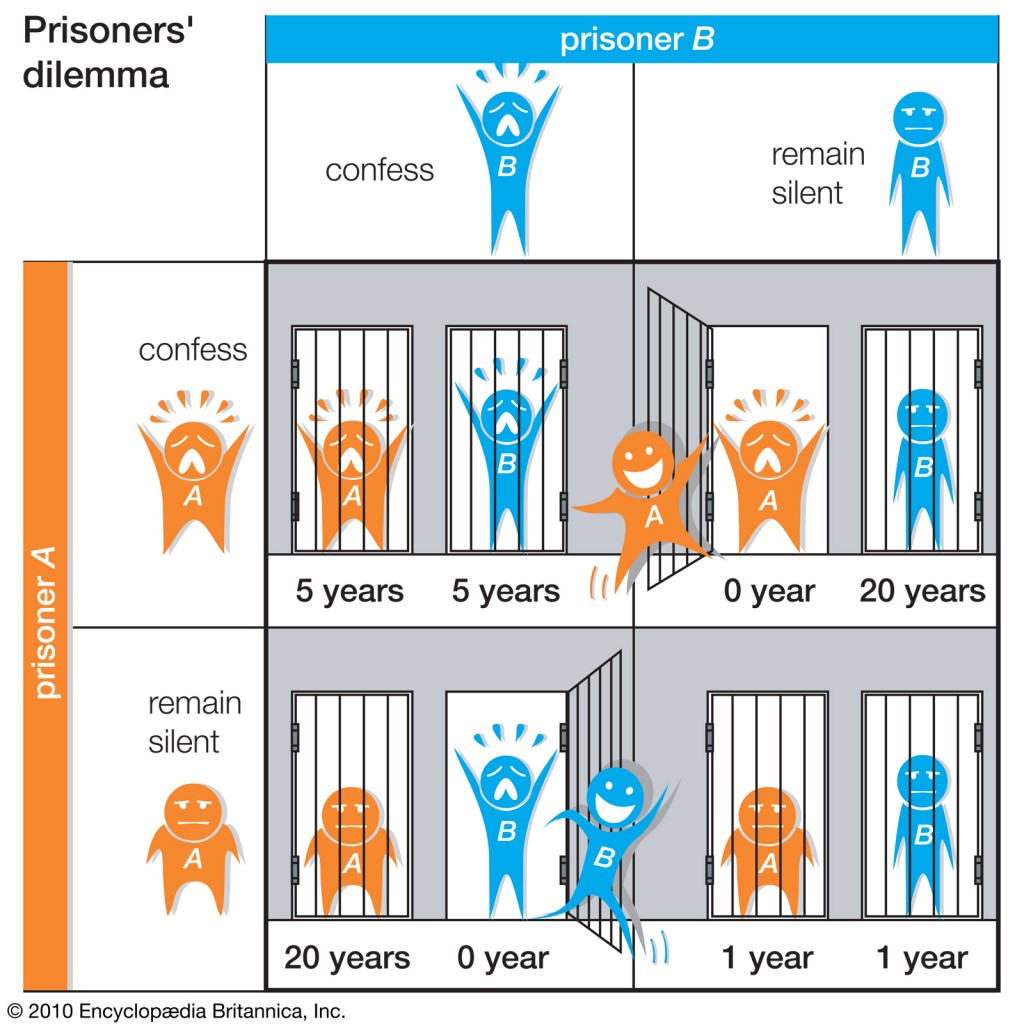
The Prisoner’s Dilemma is probably the most famous idea in game theory. Imagine two criminals have committed a crime together and have been caught by the police. The police only have enough evidence to commit the criminals of a lesser charge which would see them each spend 1 year in prison. However, the police are willing to offer the criminals a deal: if they are willing to confess against their fellow criminal, they will walk free and the other criminal will spend 20 years in prison. If both criminals confess against the other criminal, they will both spend 5 years in prison. If both criminals were to stay silent, they would each only spend one year in prison. The criminals are being kept in separate detention areas and cannot communicate. The situation is illustrated in the image below:

 

 

Given the assumptions above and some others, it turns out that the “rational” decision for both criminal’s is to confess against one another. This is because whatever the other criminal decides, the higher payoff comes from confessing against the other criminal. But this leads to a worse outcome than if both criminal’s had decided to cooperate by staying silent.

The reason this game is so famous is that it captures so much. Most importantly, it effectively models a situation where when each person pursues their own interest, they lower both their own outcome and their neighbour’s outcome. This runs contrary to the belief that both individuals and society as a whole benefit most from individuals perusing their own self interest, a belief strongly held by many.

Beliefs about the merits of cooperation vs self-interest are often very strong. One could make the argument that left vs right political debates are largely about the merits of cooperation (government action) vs self-interest (private sector).

Of course, the prisoner’s dilemma is just a model. Mathematics is a useful tool for modelling behaviour and offering explanations. When a model accurately captures reality it can be used to understand and improve upon outcomes (or at least, prevent poorer outcomes). For example, eliminating moral hazard in the finance and insurance industries. But as famed investor Warren Buffett says, “beware of geeks bearing formulas”. Bad things can happen when we rely on models that don’t accurately capture reality. Some aspects of reality are too complex to accurately model. It’s not that game theory is “bad” or “good”, it’s a powerful tool that like any other requires thoughtful use.

There has been thousands of papers written on the prisoner’s dilemma alone. I’ve left out a few assumptions in the above description. A lot of these ideas are up for debate, analysis, and further modelling. But I’ve always loved what happens when you turn the prisoner’s dilemma into an infinitely long game.

Let’s say the players in the above game were to keep playing again and again. If the players each know exactly how many times they will play the game, or if the players know their is some upper limit on the number of times the game will be played, it turns out the optimal strategy is still for the players to not cooperate. But if the players don’t know how many times they will play the game or if the game is infinitely long, it turns out that other non-selfish strategies become optimal.

 

 

There are actually “iterated prisoner’s dilemma” tournaments where computer programs employing different strategies play against one another a large number of times to explore what strategies may be optimal. More often that not it turns out that cooperative and “nice” strategies end up being optimal, rather than selfish strategies. One strategy in particular involves a player starting with cooperation, and from thereon doing in turn what the other player has done last. This is the “tit-for-tat” or the “eye for an eye” strategy. So long as the other player is using the same strategy, the players will both continue to cooperate.

Perhaps even more interestingly, it turns out that sometimes an “eye for an eye, with opportunities for forgiveness” strategy leads to even better outcomes. Why? If players are using some variant of the “eye for an eye” type strategy then it is possible to get trapped into a negative cycle, with both players trying to “punish” the other for previous transgressions. But, if with some small probability on any given turn, one player offers “forgiveness” to the other player by again cooperating, it offers both players a chance to break out of the negative cycle.

Sometimes mathematics is beautiful. Without appealing to any sort of bleeding heart sympathies, using only cold hard models and data, game theory is able to describe and capture the value of not only cooperation, but forgiveness too. However close the model is to reality, that’s pretty damn cool.